מהי בקרת איכות סטטיסטית על תהליך היצור וכיצד לבצעה?

עלינו הבוקר עם האופניים בהר חורשן. העלייה לא הייתה חדה וניתן היה לשוחח. יהושוע, מנהל מחקר ופיתוח בחברה גדולה בתחום האירוספייס, ציין כי בעזרת אוטומציה ניתן להתחרות ביצור הזול מסין. רוני, איש הייטק, ציין כי האוטומציה, מבטיחה איכות אחידה כל הזמן.

לנושא התחרות ביצור זול מסין, אדרש באחד השבועות הקרובים. באשר לאיכות אחידה ביצור עם אוטומציה, מי שמכיר מקרוב, יודע שאין ניסים. תהליך היצור משתנה כל הזמן מסיבות שונות ומגוונות.

נדרשת בקרה על התהליך, גם הבקרה יכולה להיות חלק מהאוטומציה או ידנית, ובכל מקרה היא בקרה שנבצע לאורך התהליך אחת לחצי שעה או אחת לשעה כאשר התהליך יציב. בקרה זו נשענת על עקרונות סטטיסטיים.

מדוע נדרשת בקרה גם על תהליכי יצור אוטומטיים?

לשם הפשטות אסביר את השיטה על תהליך אריזה.

נאמר שיצרן אורז שקיות של 250 גרם עדשים. היצרן נעזר במערכת משקל רב ראשית ממוחשבת. מערכת השקילה מורכבת מ-14 תאי שקילה קטנים. העדשים מוזרמים אל תאי השקילה והמחשב מחפש כל הזמן את הצירוף הקרוב ביותר של 2 עד 5 תאים שייתן 250 גרם.

זו מערכת שקילה מאד מדויקת אבל ברור לנו מתיאור השיטה שהמשקלים לא יהיו אחידים ויהיו בקירוב 250 גרם, לא בדיוק.

היצרן ישאף לתת כמה שפחות עודף משקל, שכן אנחנו, הצרכנים, משלמים רק על 250 גרם ואם יהיו בשקית 300 גרם, היצרן מפסיד הרבה כסף.

מצד שני, היצרן לא רוצה לתת פחות מ-250 גרם.

אם כך, היצרן יכייל את מערכת השקילה באופן שהשונות בין המנות שנארזות בשקיות, תהיה כמה שיותר קטנה וכמה שיותר קרובה למשקל הרשום על השקית (בדוגמה שלנו: 250 גרם).

כיצד נבצע את הבקרה על תהליך זה?

אחת לשעה, וכאשר התהליך פחות יציב, אחת לחצי שעה, מפעיל המכונה ידגום אקראית 5 שקיות שנארזו ברצף וישקול אותן.

נזכור כי שני הפרמטרים שחשובים ליצרן (כפי שראינו למעלה) הם:

1.  המשקל של השקיות. נתייחס אם כן, למשקל הממוצע של המדגם בן 5 השקיות.
2. השונות בין השקיות. נתייחס למרחק, או הטווח, בין השקית עם המשקל הגדול ביותר והשקית עם המשקל הקטן ביותר.

את שני הנתונים האלו, המפעיל רושם בטבלה ומסמן על גרף:

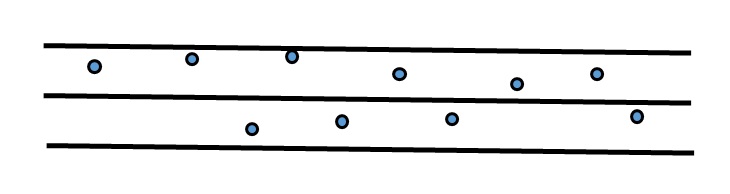
לעיתים נקבל את הנקודות (שהן ממוצע המשקלים במדגם שהמפעיל שקל) מפוזרות יותר ורחוקות מהקו האמצעי (כפי שמופיע בצד שמאל של איור 1) ולעיתים הן תהיינה קרובות יותר לקו האמצעי כפי שמופיע בצד ימין.

המטרה היא, כמובן לקבל את המשקלים (המסומנים ע"י הנקודות) סמוכים לקו האמצע, הוא קו המטרה, או הממוצע. לשם כך נכייל ונשפר את מערכת השקילה.

הקו העליון יהיה ה"גבול העליון" והקו התחתון ה"גבול התחתון".

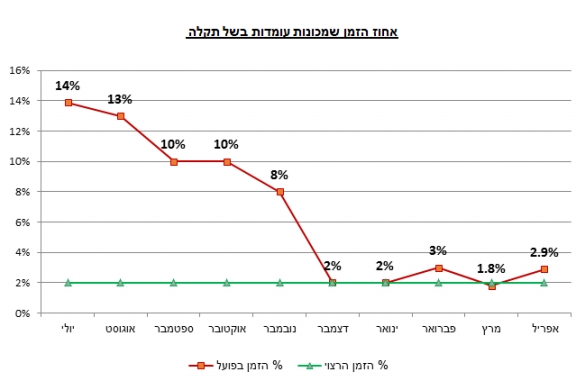
נתבונן על גרף נוסף:

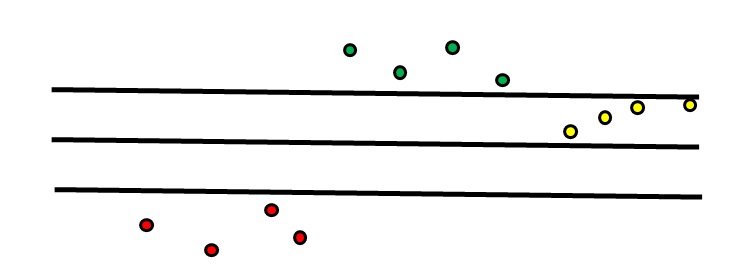
הנקודות האדומות משמאל, נמצאות מתחת לגבול התחתון והמפעיל צריך לעצור את האריזה ולכייל את המשקל או לקרא לטכנאי. כמובן שלא יהיה נכון לחכות עד שנקבל 4 מדגמים נמוכים.

מצב הפוך מדגימות הנקודות הירוקות במרכז מעל הגבול העליון והמפעיל ינהג באותו אופן.

הנקודות הצהובות, מצד ימין אמנם נמצאות בין הגבולות אך הן מציגות לנו שהתהליך הולך ויוצא מגבולות וככל הנראה קרה משהו ונדרש לעצור ולתקן.

לגבי הנקודות הצהובות מימין, נציין כי לא רק הכיוון של הנקודות בכיוון מעלה צריך להדליק לנו אור אדום.

במצב "רגיל" נצפה לקבל פיזור פחות או יותר אחיד סביב האמצע, קו המטרה (קו הממוצע). מבחינה סטטיסטית, הסיכוי לקבל נקודות רק בצד אחד של הקו, כמוהו כסיכוי למשפחה שיש בה רק 4 או 7 בנות. זה מצב אפשרי אבל הסיכוי לכך נמוך. לכן צריך להידלק לנו אור אדום וראוי לבדוק את מערכת האריזה. האם התהליך לא השתנה.

באותו אופן שהמפעיל סימן למעלה את ממוצעי השקילות שדגם, הוא יסמן את הטווח. המרחק בין המשקל הנמוך והמשקל הגבוה בכל מדגם.

עד כאן המערכת שרואה המפעיל. אך איך נגדיר את קו המטרה וקווי הגבול?

בשלב זה נרד מעט לעומק, אני מקווה להציג את ההיגיון שמאחורי השיטה באופן פשוט וברור גם למי שפחות מכיר סטטיסטיקה.

מה היא בקרת איכות סטטיסטית?

המילה סטטיסטיקה יכולה להרתיע, אך בשטח, בקו היצור, כפי שראינו למעלה, השימוש בה הוא מאד פשוט.

ראשית נציג 3 מונחים:

אוכלוסיה נורמלית: אנו מניחים כי כאשר ניקח "מספיק פריטים" של אוכלוסיה מסוימת השוני בין הפריטים יהיה עם מאפיינים דומים מאד.

המונח "מספיק פריטים" מגדיר קבוצה בה לפחות 30 פריטים (זכרו זאת, זה חשוב בהמשך להגדרת "הקווים" שהופיעו למעלה).

הפיזור של קבוצת הפריטים (או האוכלוסייה) ניקרא "פיזור נורמלי", או בשפת הסטטיסטיקה: "התפלגות נורמלית".

ניקח למשל, קבוצה של 10,000 אנשים בגילאים 15 עד 20 ונמדוד את הגובה שלהם.

תכונת הגובה של האוכלוסיה מתנהלת כ"התפלגות נורמלית".

אם הממוצע של הגובה יהיה 165 ס"מ, אזי מרבית האנשים יהיו קרובים לממוצע ומספר האנשים עם גובה נמוך יהיה קטן ויקטן ככל שהגובה ירד. הוא הדין גם עם האנשים הגבוהים. ככל שהגובה שלהם עולה, מספרם קטן.

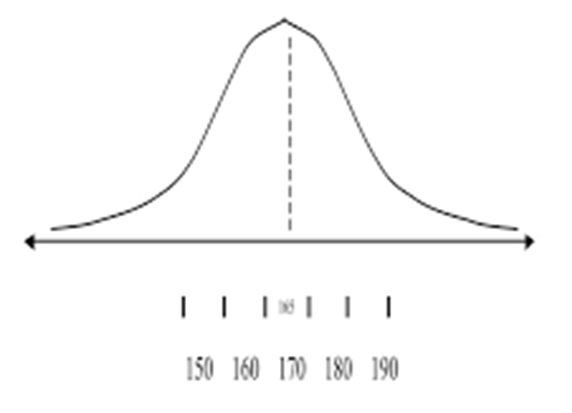
פעמון גאוס: נתבונן באיור למטה המציג את הגובה של קבוצת האנשים הזו. הפיזור של הגבהים מזכיר פעמון. הפעמון הזה נקרא "פעמון גאוס", או הפעמון של ההתפלגות הנורמלית.

הקו האופקי (ציר X) מייצג את הגבהים שנמדדו הקו האדום משמאל, הוא הציר האנכי (ציר Y), מייצג את כמות האנשים שנמדדו בגובה מסוים.

כמות האנשים באמצע היא הגדולה ביותר וככל שנלך לצדדים הכמות יורדת.

פיזור דומה נקבל כאשר נמדוד את המשקל של אותה אוכלוסיה ותכונות רבות אחרות של אוכלוסיות בהן מספר הפריטים רב (כזכור, מעל 30 פריטים).

כפי שראינו למעלה הפיזור של הנקודות (שמייצגות את התכונה שנמדדה, למשל הגובה של האנשים או ממוצע המשקלים בכל מדגם של שקיות העדשים) אינו אחיד.

סטיית תקן: אנו מודדים את שונות הפיזור ע"י תכונה שנקראת "סטיית תקן" ומסמנים אותה ע"י האות היוונית סיגמא קטנה: σ.

סטיית התקן מייצגת לנו, פחות או יותר, את הממוצע של המרחקים של כלל הנקודות מהאמצע, מהממוצע.

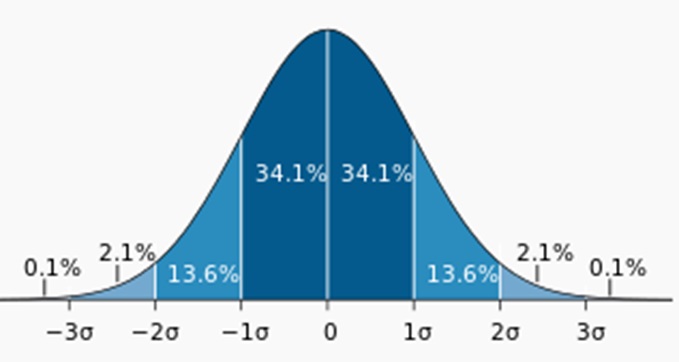
נתבונן כעת על האיור למטה.

נמדוד ונסמן משני הצדדים של קו הממוצע, הקו באמצע, על הציר האופקי, מרחקים באורך של סטיית תקן.

נסמן ימינה מרחק של סטיית תקן אחת, שתי סטיות ושלש. באותו אופן נמדוד ונסמן שמאלה.

תכונה נוספת שמאפיינת את "האוכלוסיות הנורמליות", פרט לפיזור בצורה של פעמון גאוס, היא שבמרחק ימינה ושמאלה של סטיית תקן אחת מקו האמצע, נקבל 68% מהאוכלוסיה.

אם נלך עוד סטיית תקן אחת ימינה ושמאלה, נקבל שבטווח של 2 סטיות תקן ימינה ושמאלה, אנו מקבלים 95.4% מהאוכלוסיה.

נחזור לשקיות העדשים.

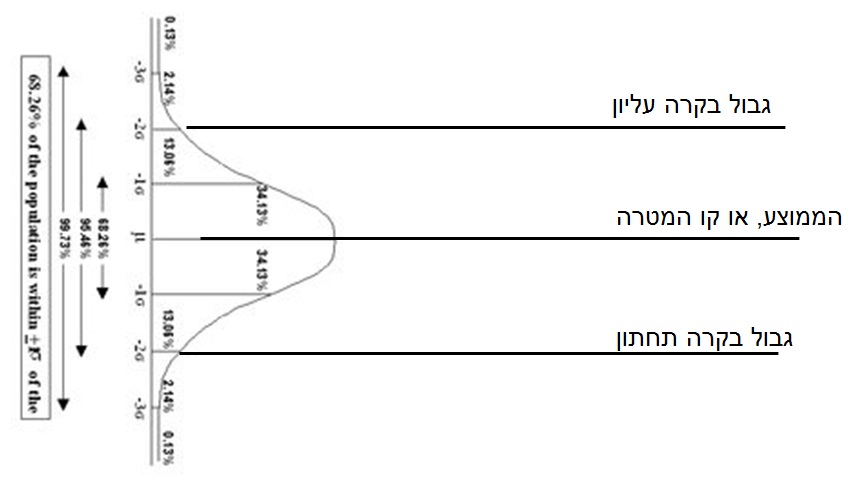
נתבונן באיור למטה. סובבתי את פעמון גאוס על הצד ומשכתי את הקווים המסמנים את הממוצע ואת המרחק של 2 סטיות תקן מכל צד של קו הממוצע.

אנחנו מניחים, אם כן, ש-95.4% מהאוכלוסיה של שקיות העדשים שנארזות, תהיינה בין הגבול התחתון והעליון.

או, אם נתבונן על כך מהכיוון השני, הסיכוי לקבל שקילה מחוץ לגבולות הוא פחות מ-5%. לכן אם קיבלנו שם נקודת שקילה, מרבית הסיכויים שמערכת האריזה השתנתה ואנחנו מקבלים כעת "אוכלוסיה אחרת" ולכן צריך לכייל את מערכת האריזה, את המשקל הרב ראשי הממוחשב אותו הצגתי למעלה.

איך מוצאים את המאפיינים של פעמון הגאוס, את הממוצע והגבולות?

זוכרים שהגדרנו למעלה שאוכלוסיה של 30 פריטים היא כבר "מספיק גדולה" כדי ליצור את "הפיזור הנורמלי"? ובכן, בתחילת התהליך שוקלים 30 שקיות, מחשבים את הממוצע ואת סטיות התקן (חישוב של סטיית תקן הינו פונקציה סטנדרטית במחשבונים רבים ובוודאי שבגיליון אקסל) מסמנים את הקווים על ניר הבקרה והמפעיל יכול להתחיל בבקרה.

על נייר העבודה רצוי לא לרשום את פעמון הגאוס כדי לא להרתיע את המפעילים.

אני כן ממליץ להדריך ולהסביר למפעילים את הרקע לשיטת הבקרה.

סיכום:

שיטת העבודה שהדגמתי כאן על שקיות עדשים נכונה בכל תהליך ובכלל זה מכונות לעיבוד שבבי מבוקרות מחשב (CNC) וכל תהליך אוטומטי אחר.

אין עובדים שלא יוכלו לבצע את הבקרה הסטטיסטית שהצגתי כאן.

הדרכה נכונה וליווי בתחילת הדרך יאפשרו לכל עובד ללמוד את אופן העבודה. יתר על כן, עבודה זו מוסיפה משמעות רבה לעבודת המפעיל (בתנאי שנתנו לו רקע והסבר סבלני), ומכאן מעלה את המוטיבציה של העובד והמחויבות שלו ליצר תוצרת איכותית.

כרגיל, אני זמין לפניות של הקוראים להסבר נוסף ושאלות ותשובות.